“Michael Covel’s Trend Following: Essential.”
–Ed Seykota, Market Wizard
The Wall Street industrial complex wants to bleed you dry. Michael Covel gives traders a way out. He teaches newbies to pros how to trade stocks, rates, currencies, metals, energies, futures, commodities, ETFs and crypto as a trend following trader. No fundamentals. No news. No 1-hour bars. No day trading. No predictions. No charting. No candles. No bullshit.
Take Michael's trading course now.
Trend following is your opportunity for outsized profits in bull, bear and black swan markets. Let go of what you think you know and learn how the Market Wizards really do it.
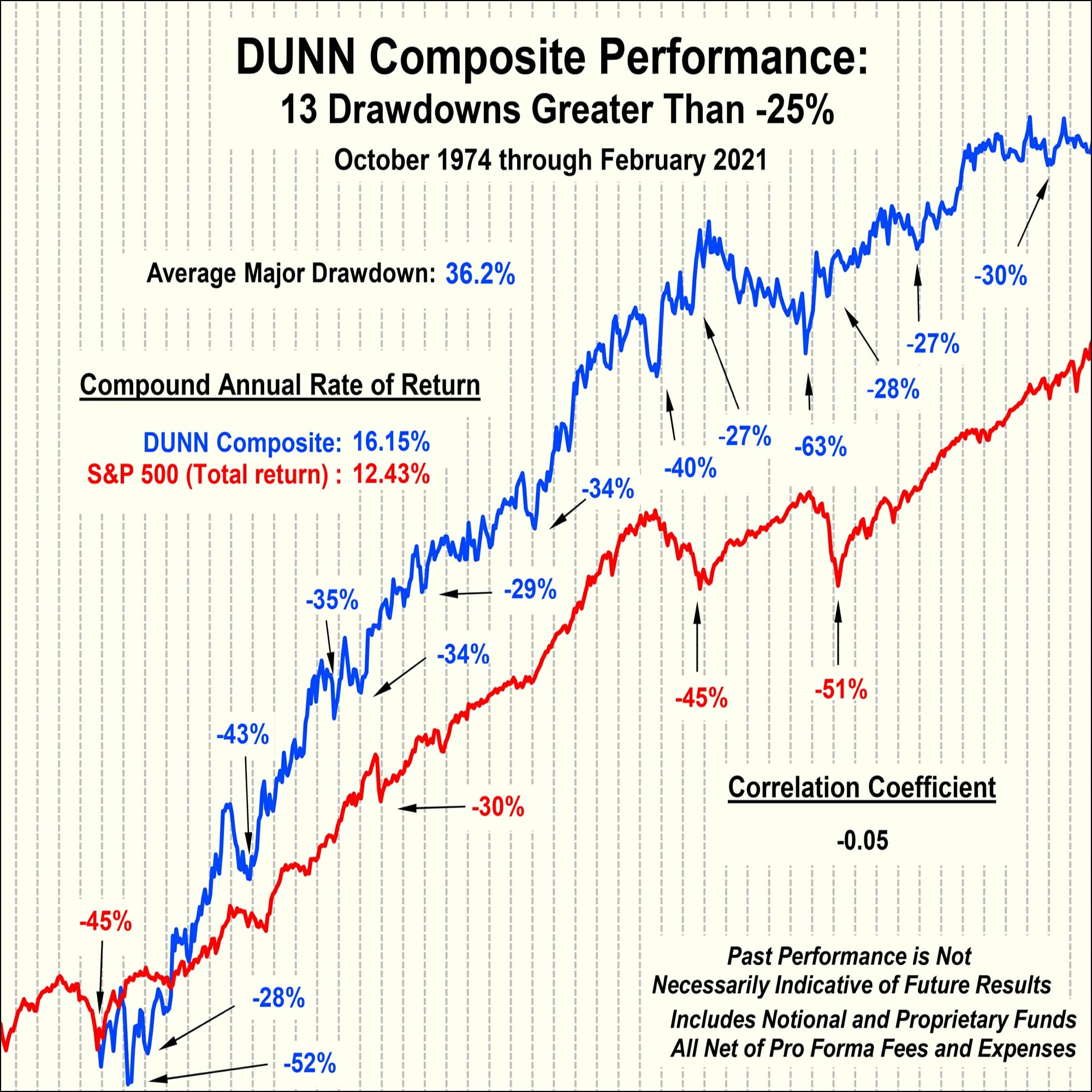
Performance | Big Events | Charts | Zero Sum
More than 500,000+ investors and traders across 70+ countries have read Michael Covel’s 8 books and taken his 3 trading courses.
FAQS
The Details: 15 million + listens. 1100 + episodes. Continuous since 2012.
Topics: Freedom. Liberty. Trading. Investments. Economics. Psychology. Risk-Taking. Human Behavior. Decision-Making. Entrepreneurship. Culture. Philosophy.
Trading Guests: Ed Seykota, Jerry Parker, Ewan Kirk, Jim Rogers, Jack Schwager, Howard Marks, Larry Hite, Mebane Faber, Alexander Elder, Tom Basso, John Bollinger, Larry Williams, Marc Faber, Martin Lueck + 100s more.
Nobel Prize Guests: Robert Aumann, Angus Deaton, Daniel Kahneman, Harry Markowitz, Paul Nurse, Oliver Hart & Vernon Smith.
Notable Guests: Jack Canfield, Robert Cialdini, Tim Ferriss, Jason Fried, Gerd Gigerenzer, Ryan Holiday, Jack Horner, Barry Ritholtz, Philip Tetlock, Walter Williams, Tucker Max, Steven Pinker, Alison Gopnik, Annie Duke, Anders Ericsson, Michael Mauboussin, Bill Bonner, Nolan Bushnell + 100s more.
The true story of nurture beating nature.

Learn from a Market Wizard legend.